Moderation analysis
Three moderation analyses are supported:
Two types of graphs are available for moderation analyses.
For case 1, one of each type will be produced, for the other two cases three
graphs of each type will be produced. Definitions for elements of the graphs
are given for Case 1 but applies equally to the other two cases.
Case 1: One moderator
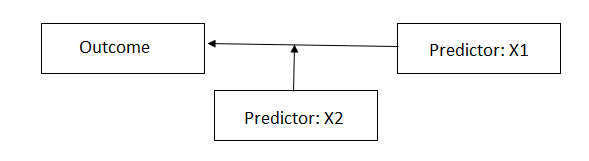 In Case 1, the predictor or moderator variable X2 moderates
the relationship between the focal variable X1 and the outcome. This
corresponds to the equation
In Case 1, the predictor or moderator variable X2 moderates
the relationship between the focal variable X1 and the outcome. This
corresponds to the equation
 The program can accommodate a same level interaction term
such as X1*X2 at any level of the model. Below are two examples of
moderation analyses of this type of model. Either of the two predictors in a
model can be selected as the focal variable, with the remaining variable
serving as moderator variable. The choice is dependent on the researcher’s
theoretical framework.
The program can accommodate a same level interaction term
such as X1*X2 at any level of the model. Below are two examples of
moderation analyses of this type of model. Either of the two predictors in a
model can be selected as the focal variable, with the remaining variable
serving as moderator variable. The choice is dependent on the researcher’s
theoretical framework.
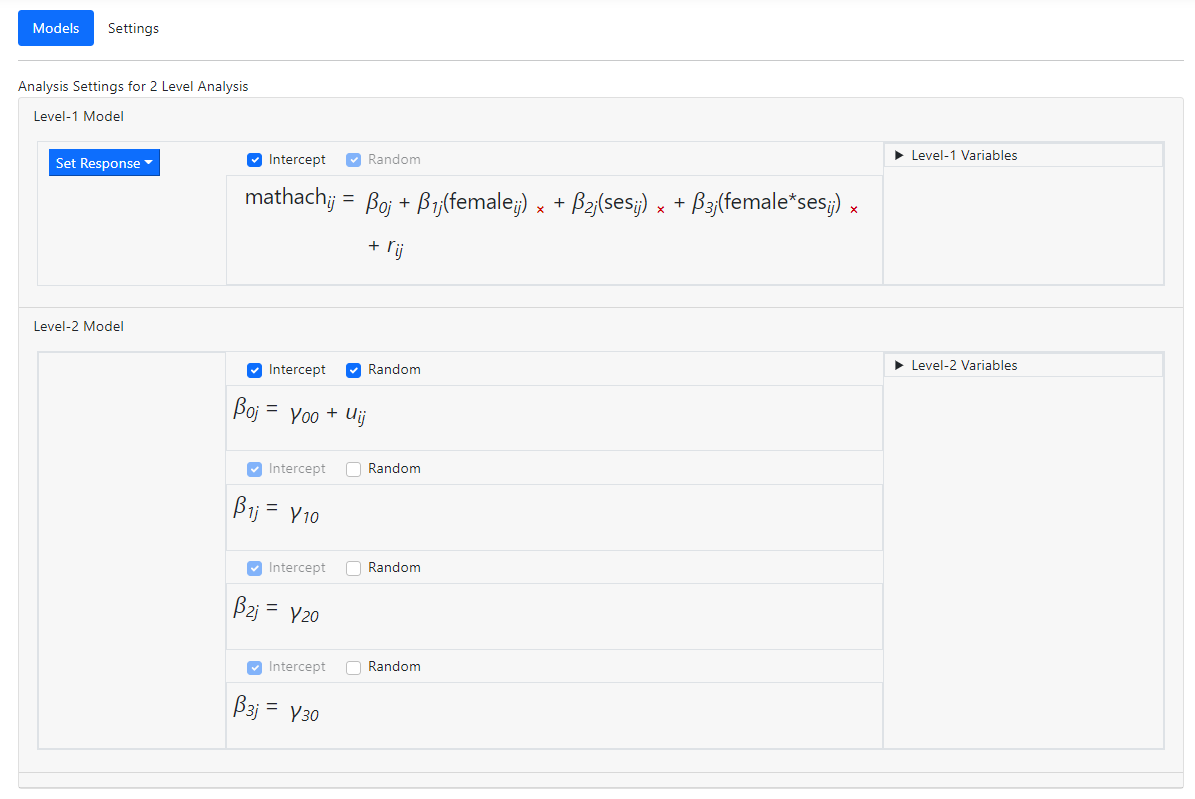
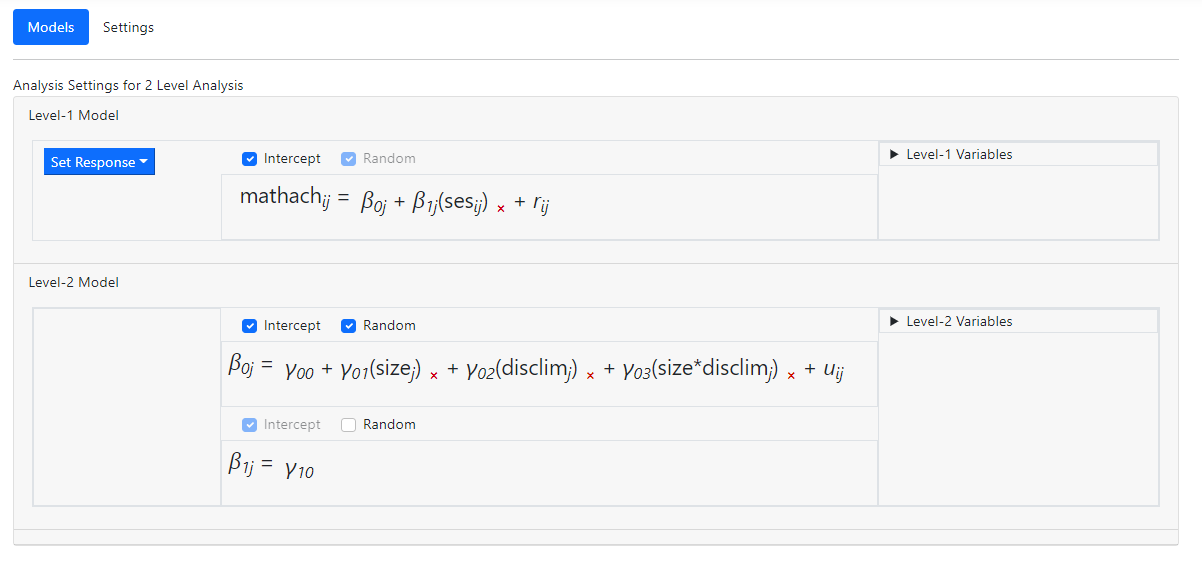 To request graphs, the focal and moderator variables are
specified on the Settings page as shown below before accessing the Graphing
page.
To request graphs, the focal and moderator variables are
specified on the Settings page as shown below before accessing the Graphing
page.
 Simple slopes graph:
The first of the available graphs is a plot of the conditional regression line(s) describing the relationship between the outcome and the focal predictor as a function of the moderator. The plot will automatically show a line at each of three values of the moderator variable: mean – 1 standard deviation, mean, and mean + 1 standard deviation. In other words, the value of the moderator variable is held constant at three specific values. Values of the focal variable are used to define the x-axis, and the plot is confined to the area (mean of focal variable – 2 standard deviations, mean of focal variable + 2 standard deviations). Here is an
example of a simple slopes graph using default graph parameter settings:
Simple slopes graph:
The first of the available graphs is a plot of the conditional regression line(s) describing the relationship between the outcome and the focal predictor as a function of the moderator. The plot will automatically show a line at each of three values of the moderator variable: mean – 1 standard deviation, mean, and mean + 1 standard deviation. In other words, the value of the moderator variable is held constant at three specific values. Values of the focal variable are used to define the x-axis, and the plot is confined to the area (mean of focal variable – 2 standard deviations, mean of focal variable + 2 standard deviations). Here is an
example of a simple slopes graph using default graph parameter settings:
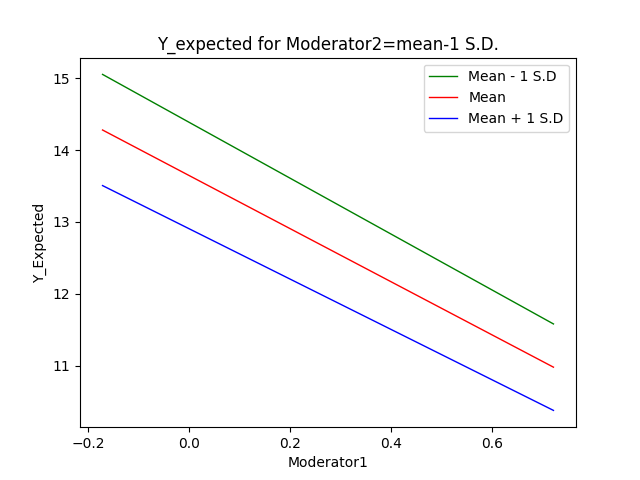 The graph is produced as a *.png file which can
easily be inserted into a paper. A number of graph settings may also be
modified by the user on the Graphing page within the program. To access
the graphs, use the Run page.
Confidence interval graph:
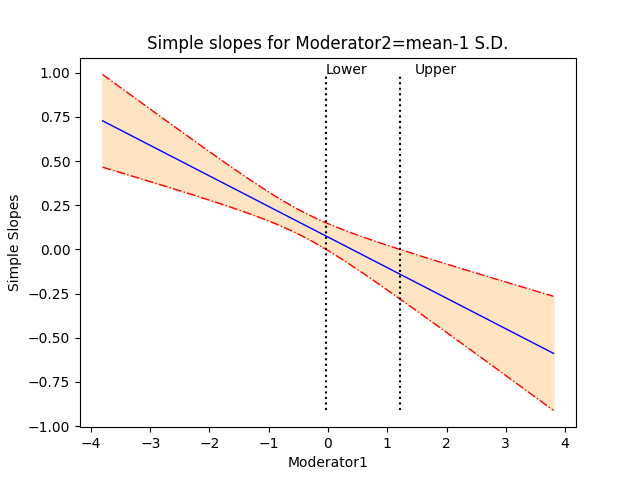
The second graph shows the regression line describing the
relationship between the outcome and the focal predictor as a function of the
moderator, along with a 95% confidence interval. It also shows the so-called
region of significance, provided that the boundaries of this region fall within
the scale set by the values of the moderator variable, which again defines the
x-axis. The region between the lower and upper bound of the region of significance
indicates the values of the moderator for which the slope of the regression of
outcome on focal variable transitions from non-significance to significance.
An example of the confidence interval graph with regions of significance
is shown below.
The graph is produced as a *.png file which can
easily be inserted into a paper. A number of graph settings may also be
modified by the user on the Graphing page within the program. To access
the graphs, use the Run page.
Confidence interval graph:
The second graph shows the regression line describing the
relationship between the outcome and the focal predictor as a function of the
moderator, along with a 95% confidence interval. It also shows the so-called
region of significance, provided that the boundaries of this region fall within
the scale set by the values of the moderator variable, which again defines the
x-axis. The region between the lower and upper bound of the region of significance
indicates the values of the moderator for which the slope of the regression of
outcome on focal variable transitions from non-significance to significance.
An example of the confidence interval graph with regions of significance
is shown below.
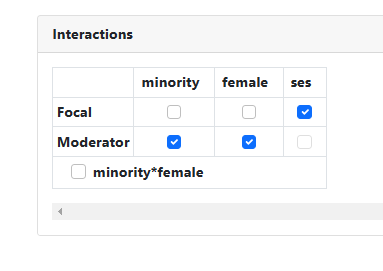
Case 2: Two independent moderators
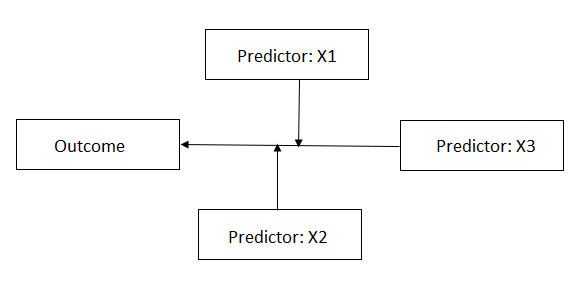
Consider the case where the relationship between the outcome
and a predictor (denoted as X3 in the image below) is moderated by two
predictors (X1 and X2). While it is assumed that these two variables moderate
the relationship, they are independent of each other.
 This corresponds to the equation
This corresponds to the equation
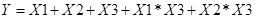 Again, focal and moderator variables may be at any level of
the hierarchy. Here is an example of such a model, occurring at level-1 of the
hierarchy. The relationship between the outcome MATHACH and the focal variable
SES is moderated by the two independent variables MINORITY and FEMALE.
Again, focal and moderator variables may be at any level of
the hierarchy. Here is an example of such a model, occurring at level-1 of the
hierarchy. The relationship between the outcome MATHACH and the focal variable
SES is moderated by the two independent variables MINORITY and FEMALE.
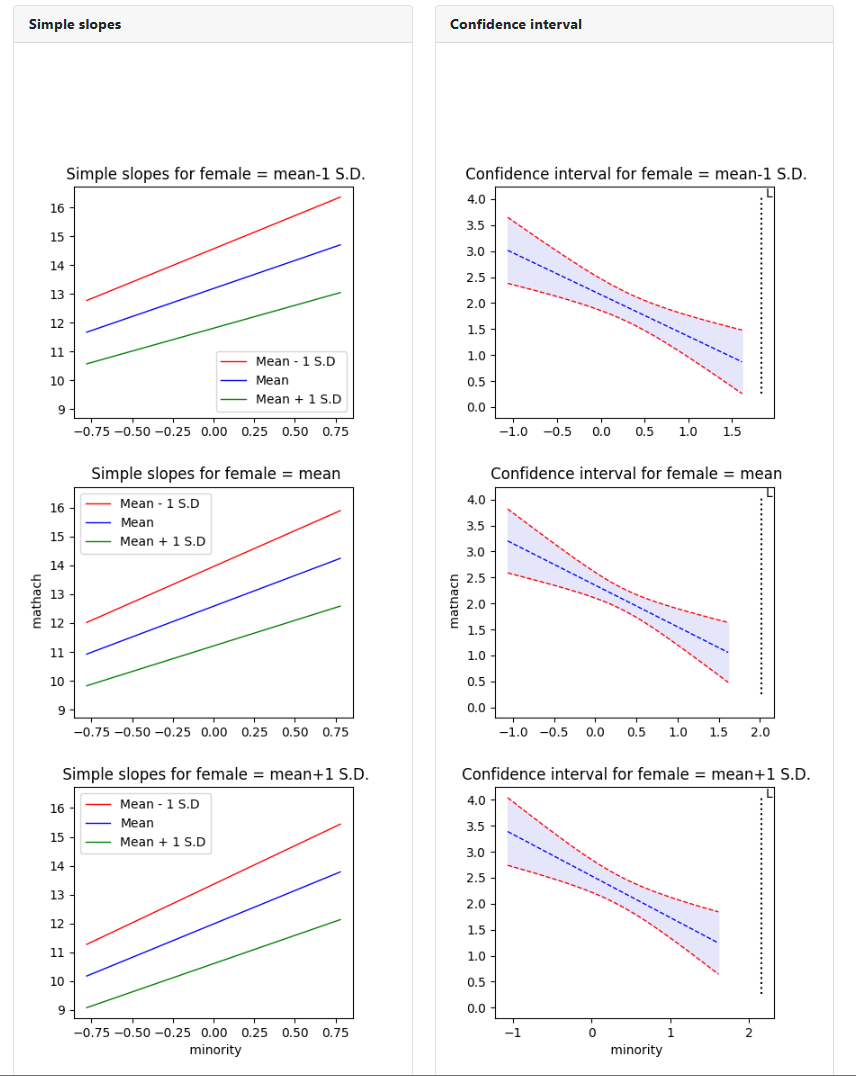
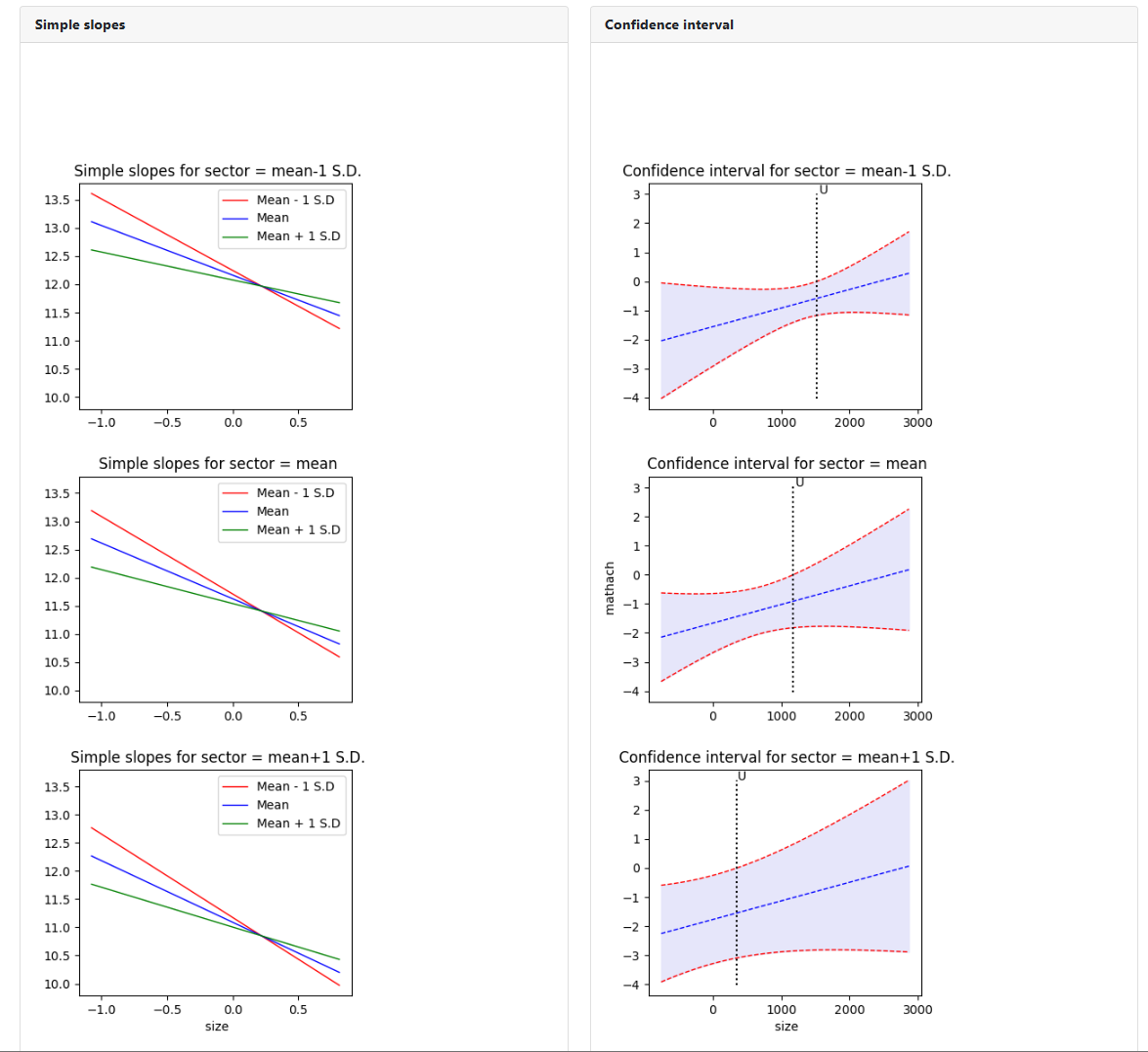
 In this case, three simple slopes and three confidence
interval graphs are produced, one for each of three values of the second
moderator variable. Similarly, three confidence interval graphs are produced,
as shown below. In all cases, values of the first moderator variables define
the x-axis.
In this case, three simple slopes and three confidence
interval graphs are produced, one for each of three values of the second
moderator variable. Similarly, three confidence interval graphs are produced,
as shown below. In all cases, values of the first moderator variables define
the x-axis.
 To access the graphs, use the Run
page. Note that they can also be downloaded together with all files
used in the analysis. To change graph parameters, use the Graphing page. The graphs will
be displayed on the Run page, from where they may be copied as well.
To access the graphs, use the Run
page. Note that they can also be downloaded together with all files
used in the analysis. To change graph parameters, use the Graphing page. The graphs will
be displayed on the Run page, from where they may be copied as well.
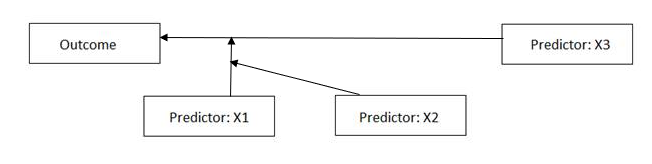
Case 3: Two dependent moderators
In this case, there are again two predictors moderating the
relationship between the outcome and a focal predictor (denoted as X3) in the
image below. However, in contrast with Case 2, where two independent moderators
are present, here the two moderators X1 and X2 are dependent.
 This corresponds to the equation
This corresponds to the equation
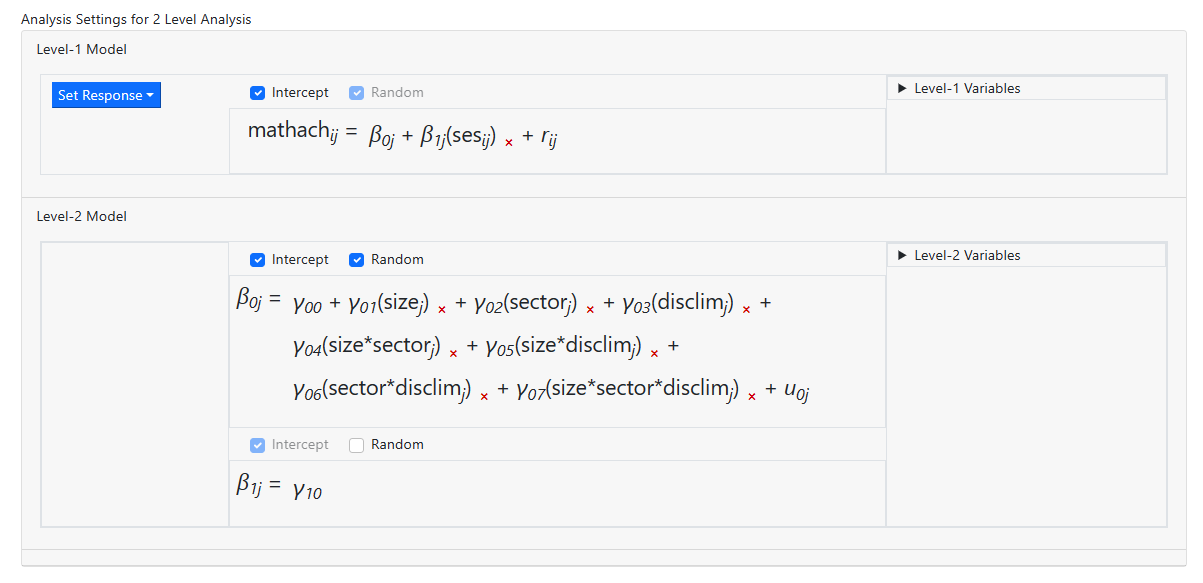
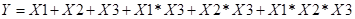 Case 3 includes two-way interaction terms and a three-way interaction
term between the focal variable (X3) and the two moderators (X1,X2). Below is
an example of such a moderation analysis set up on the intercept equation at
level-2. The variable DISCLIM serves as the focal variable, with SIZE and
SECTOR the two dependent moderators.
Case 3 includes two-way interaction terms and a three-way interaction
term between the focal variable (X3) and the two moderators (X1,X2). Below is
an example of such a moderation analysis set up on the intercept equation at
level-2. The variable DISCLIM serves as the focal variable, with SIZE and
SECTOR the two dependent moderators.
 There is again no restriction in terms of which level this
may be specified at. Keep in mind that the program does not allow any
higher-level interaction than a three-way interaction, so while it is possible
to specify this model on, say, the intercept equation at a higher level, it
will not be possible to do so on a slope equation.
Graphs produced for this case are like those produced in
Case 2: 3 simple slope graphs, and three confidence intervals graphs are
created. To change graph parameters, use the Graphing
page. The graphs will be displayed on the Run page, from where they may
be copied as well.
There is again no restriction in terms of which level this
may be specified at. Keep in mind that the program does not allow any
higher-level interaction than a three-way interaction, so while it is possible
to specify this model on, say, the intercept equation at a higher level, it
will not be possible to do so on a slope equation.
Graphs produced for this case are like those produced in
Case 2: 3 simple slope graphs, and three confidence intervals graphs are
created. To change graph parameters, use the Graphing
page. The graphs will be displayed on the Run page, from where they may
be copied as well.
 In Case 1, the predictor or moderator variable X2 moderates
the relationship between the focal variable X1 and the outcome. This
corresponds to the equation
In Case 1, the predictor or moderator variable X2 moderates
the relationship between the focal variable X1 and the outcome. This
corresponds to the equation
 The program can accommodate a same level interaction term
such as X1*X2 at any level of the model. Below are two examples of
moderation analyses of this type of model. Either of the two predictors in a
model can be selected as the focal variable, with the remaining variable
serving as moderator variable. The choice is dependent on the researcher’s
theoretical framework.
The program can accommodate a same level interaction term
such as X1*X2 at any level of the model. Below are two examples of
moderation analyses of this type of model. Either of the two predictors in a
model can be selected as the focal variable, with the remaining variable
serving as moderator variable. The choice is dependent on the researcher’s
theoretical framework.

 To request graphs, the focal and moderator variables are
specified on the Settings page as shown below before accessing the Graphing
page.
To request graphs, the focal and moderator variables are
specified on the Settings page as shown below before accessing the Graphing
page.
 Simple slopes graph:
The first of the available graphs is a plot of the conditional regression line(s) describing the relationship between the outcome and the focal predictor as a function of the moderator. The plot will automatically show a line at each of three values of the moderator variable: mean – 1 standard deviation, mean, and mean + 1 standard deviation. In other words, the value of the moderator variable is held constant at three specific values. Values of the focal variable are used to define the x-axis, and the plot is confined to the area (mean of focal variable – 2 standard deviations, mean of focal variable + 2 standard deviations). Here is an
example of a simple slopes graph using default graph parameter settings:
Simple slopes graph:
The first of the available graphs is a plot of the conditional regression line(s) describing the relationship between the outcome and the focal predictor as a function of the moderator. The plot will automatically show a line at each of three values of the moderator variable: mean – 1 standard deviation, mean, and mean + 1 standard deviation. In other words, the value of the moderator variable is held constant at three specific values. Values of the focal variable are used to define the x-axis, and the plot is confined to the area (mean of focal variable – 2 standard deviations, mean of focal variable + 2 standard deviations). Here is an
example of a simple slopes graph using default graph parameter settings:
 The graph is produced as a *.png file which can
easily be inserted into a paper. A number of graph settings may also be
modified by the user on the Graphing page within the program. To access
the graphs, use the Run page.
Confidence interval graph:
The second graph shows the regression line describing the
relationship between the outcome and the focal predictor as a function of the
moderator, along with a 95% confidence interval. It also shows the so-called
region of significance, provided that the boundaries of this region fall within
the scale set by the values of the moderator variable, which again defines the
x-axis. The region between the lower and upper bound of the region of significance
indicates the values of the moderator for which the slope of the regression of
outcome on focal variable transitions from non-significance to significance.
An example of the confidence interval graph with regions of significance
is shown below.
The graph is produced as a *.png file which can
easily be inserted into a paper. A number of graph settings may also be
modified by the user on the Graphing page within the program. To access
the graphs, use the Run page.
Confidence interval graph:
The second graph shows the regression line describing the
relationship between the outcome and the focal predictor as a function of the
moderator, along with a 95% confidence interval. It also shows the so-called
region of significance, provided that the boundaries of this region fall within
the scale set by the values of the moderator variable, which again defines the
x-axis. The region between the lower and upper bound of the region of significance
indicates the values of the moderator for which the slope of the regression of
outcome on focal variable transitions from non-significance to significance.
An example of the confidence interval graph with regions of significance
is shown below.

 This corresponds to the equation
This corresponds to the equation
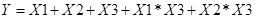 Again, focal and moderator variables may be at any level of
the hierarchy. Here is an example of such a model, occurring at level-1 of the
hierarchy. The relationship between the outcome MATHACH and the focal variable
SES is moderated by the two independent variables MINORITY and FEMALE.
Again, focal and moderator variables may be at any level of
the hierarchy. Here is an example of such a model, occurring at level-1 of the
hierarchy. The relationship between the outcome MATHACH and the focal variable
SES is moderated by the two independent variables MINORITY and FEMALE.
 In this case, three simple slopes and three confidence
interval graphs are produced, one for each of three values of the second
moderator variable. Similarly, three confidence interval graphs are produced,
as shown below. In all cases, values of the first moderator variables define
the x-axis.
In this case, three simple slopes and three confidence
interval graphs are produced, one for each of three values of the second
moderator variable. Similarly, three confidence interval graphs are produced,
as shown below. In all cases, values of the first moderator variables define
the x-axis.
 To access the graphs, use the Run
page. Note that they can also be downloaded together with all files
used in the analysis. To change graph parameters, use the Graphing page. The graphs will
be displayed on the Run page, from where they may be copied as well.
To access the graphs, use the Run
page. Note that they can also be downloaded together with all files
used in the analysis. To change graph parameters, use the Graphing page. The graphs will
be displayed on the Run page, from where they may be copied as well.
 This corresponds to the equation
This corresponds to the equation
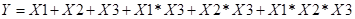 Case 3 includes two-way interaction terms and a three-way interaction
term between the focal variable (X3) and the two moderators (X1,X2). Below is
an example of such a moderation analysis set up on the intercept equation at
level-2. The variable DISCLIM serves as the focal variable, with SIZE and
SECTOR the two dependent moderators.
Case 3 includes two-way interaction terms and a three-way interaction
term between the focal variable (X3) and the two moderators (X1,X2). Below is
an example of such a moderation analysis set up on the intercept equation at
level-2. The variable DISCLIM serves as the focal variable, with SIZE and
SECTOR the two dependent moderators.
 There is again no restriction in terms of which level this
may be specified at. Keep in mind that the program does not allow any
higher-level interaction than a three-way interaction, so while it is possible
to specify this model on, say, the intercept equation at a higher level, it
will not be possible to do so on a slope equation.
Graphs produced for this case are like those produced in
Case 2: 3 simple slope graphs, and three confidence intervals graphs are
created. To change graph parameters, use the Graphing
page. The graphs will be displayed on the Run page, from where they may
be copied as well.
There is again no restriction in terms of which level this
may be specified at. Keep in mind that the program does not allow any
higher-level interaction than a three-way interaction, so while it is possible
to specify this model on, say, the intercept equation at a higher level, it
will not be possible to do so on a slope equation.
Graphs produced for this case are like those produced in
Case 2: 3 simple slope graphs, and three confidence intervals graphs are
created. To change graph parameters, use the Graphing
page. The graphs will be displayed on the Run page, from where they may
be copied as well.
